Worm and wheel systems are no more and no less than crossed axle helical gear system which has a drive wheel with a maximum of six teeth. Which is called in this case a worm.
The calculation of the reduction ratio is exactly the same. As there are very few teeth on the drive wheel (worm), it can be seen that the reduction ratios can be very high. This is the major advantage of this system : With just two elements, it is possible to considerably reduce the speed.

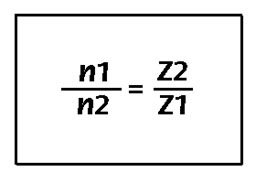
The efficiency of such a system is not very good. It increases with the slope angle of the tooth. There are high levels of friction, and part of the kinetic energy is transformed into heat. In order to limit the friction levels, the wheel is usually made out of bronze.

Lubrication either with grease or with oil is a necessity.

gold stone proposes two different kinds of worm, bored or shaft mounted. The difference is in the assembly. Its enough to pass a shaft through a bored worm to get a shaft mounted version. See worms W, SW, SWH. By reading the formulas opposite one can see that the Helical angle is highly significant in such a system. In effect, the diameter of the worm and the HA are mathematically linked. In fact, in the case of a breakage, the defective piece (normally the wheel) must be replaced by an absolutely identical componant. Most of the time the piece must be made to order. As well as that, the number of threads (starts) on the worm influences the HA. This angle is linked to the wheel angle, which must be designed for use with a 2,3, or 4 thread/start worm.	Geometrical formulas for the worm :
	Axial module : mx=mn/cos?/FONT>
	Axial pitch : px=mx
	Helical pitch : pz=pxz
	pitch diameter : d=pz/tan?/FONT>
	external diameter : da=d+2mn
	root diameter: df=d-2.5mn
	Geometrical formulas for the wheel :
	See helical gears
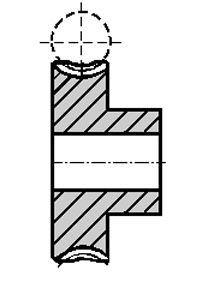Wheels Symbols Formulas Unit Module m p   mm Pitch p m x mm Pitch diameter d Z x m mm Number of teeth Z d  m External diameter dc (Z + 2) x m mm	Wheel M
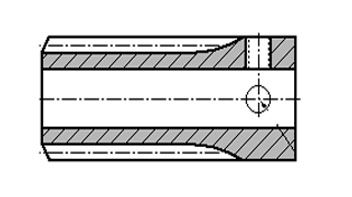
Worms Symbols Formulas Unit Outer diameter D (2 x m) + d mm The tangent to the lead angle ?/FONT> (m x Z)  d Pitch diameter d p x Z tan?/FONT> mm Center to center d(wheel) + d(worm) 2	Worm W and WH Worm SW and SWH
with bored worm	with shafted worm

• Gives very high reduction ratios
• Irrsible in certain circumstances
• Helical Angles must be equal
• The direction of the lead angle must be the same for the wheel and for the worm (to change direction by 90?
• Not very efficient (from 40% to 70%) depending on the material and the lubrication.